K-Means算法是最基础的聚类算法、也是最常用的机器学习算法之一。 本教程中,我们利用K-Means对图像中的像素点进行聚类,然后用每个像素所在的簇的中心点来代替每个像素的真实值,从而达到图像压缩的目的。
非负矩阵分解(Non-negative Matrix Factorization, NMF)是一种对非负矩阵进行低维近似逼近的常见方法,同样也能达到图像压缩的目的。
预计学习用时:30分钟。
本教程基于Python 3.5。
原创者:SofaSofa TeamM | 修改校对:SofaSofa TeamC |
前言
K Means算法比NMF算法慢很多,尤其是当聚类数较大时,所以实验时请耐心等待。此外,由于两者重建图像的原理不同,所以两者的视觉也相差很大,k Means牺牲了颜色的个数而保留了边界和形状,而NMF牺牲了形状以及边界却尽量保留颜色。整个实验过程中会产生一些有趣风格的图像,注意留意哦!
完整的代码在第4节。
- 图像的读取
本教程以台湾省台北市最高建筑“台北101”大厦的夜景图为例,该图的分辨率为600 * 800。
点击这里下载实验图片。
我们需要skimage、numpy、matplotlib.pyplot这三个库来实现图像的读取以及显示。import numpy as np import matplotlib.pyplot as plt from skimage import io
利用
io.imread直接读取图像文件,并存入np.ndarray类型的变量d。注意:为了图像在plt中无色差地显示,请一定要将d中的元素转成0到1的浮点数。d = io.imread('taibei101.jpg') d = np.array(d, dtype=np.float64) / 255d是三维array,第一个维度代表行数,第二个维度代表列数,第三个维度代表该图像是RGB图像,每个像素点由三个数值组成。
d.shape (600, 800, 3)
调用plt.imshow函数便可以显示图像。
plt.axis('off') plt.imshow(d); plt.show()
K Means 压缩图像
在我们的例子当中,每个像素点都是一个数据;每个数据拥有三个特征,分别代表R(红色),G(绿色),B(蓝色)。 K Means是一种常见的聚类方法,其思想就是让“距离”近的数据点分在一类。这里的“距离”就是指两个像素点RBG差值的平方和的根号。
Dist(P1,P2)=∥P1−P2∥2
K Means压缩图像的原理是,用每个聚类(cluster)的中心点(center)来代替聚类中所有像素原本的颜色,所以压缩后的图像只保留了K个颜色。
假如这个600×800的图像中每个像素点的颜色都不一样,那么我们需要
800×600×3=1440000
个数来表示这个图像。对于K Means压缩之后的图像,我们只需要
800×600×1+K×3
个数来表示。800×600×1是因为每个像素点需要用一个数来表示其归属的簇,K×3是因为我们需要记录K个中心点的RGB数值。所以经过K Means压缩后,我们只需要三分之一左右的数就可以表示图像。
下面的函数KMeansImage(d, n_colors)就可以用来生成n_colors个颜色构成的图像。
from sklearn.cluster import KMeans
def KMeansImage(d, n_colors):
w, h, c = d.shape
dd = np.reshape(d, (w * h, c))
km = KMeans(n_clusters=n_colors)
km.fit(dd)
labels = km.predict(dd)
centers = km.cluster_centers_
new_img = d.copy()
for i in range(w):
for j in range(h):
ij = i * h + j
new_img[i][j] = centers[labels[ij]]
return {'new_image': new_img, 'center_colors': centers}
运行以上函数,我们可以看看在不同的K的取值之下,图像压缩的效果。
plt.figure(figsize=(12, 9))
plt.imshow(d); plt.axis('off')
plt.show()
for i in [2, 3, 5, 10, 30]:
print('Number of clusters:', i)
out = KMeansImage(d, i)
centers, new_image = out['center_colors'], out['new_image']
plt.figure(figsize=(12, 1))
plt.imshow([centers]); plt.axis('off')
plt.show()
plt.figure(figsize=(12, 9))
plt.imshow(new_image); plt.axis('off')
plt.show()
Number of clusters: 2


Number of clusters: 3
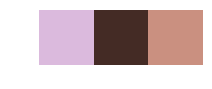

Number of clusters: 5


Number of clusters: 10
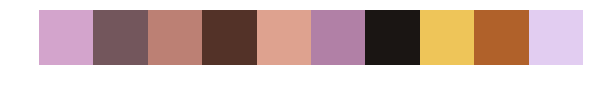

Number of clusters: 30






文章评论